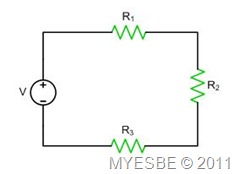
Voltage Divider Rule (VDR)

 

Voltage Divider Rule (VDR) is only valid for a series circuit as shown in figure below. VDR is used to calculate the voltage at any one of the resistor. By using VDR, summation of all voltages from each resistor will equal to the voltage source as what has been stated by KVL. The voltage division starts from the main source and continue till end of the circuit.

VDR:

VR1 = [R1/(R1 + R2 + R3)] * V;

VR2 = [R2/(R1 + R2 + R3)] * V;

VR3 = [R3/(R1 + R2 + R3)] * V;

KVL:

V = VR1 + VR2 + VR3

 

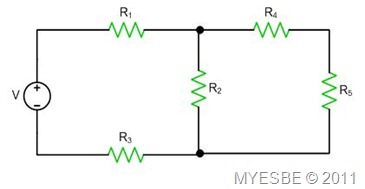
If we have a circuit as shown in figure below, in order to find VR2 we have to simplify it until it becomes a series circuit before VDR can be used. Therefore VR2 is basically the voltage across total resistance R2&4&5. It’s happen because VR2 is equal to VR4&5 and they are connected in parallel.

So, VR2 = [R2&4&5/(R1 + R2&4&5 + R3)] * V;

To calculate VR5 or VR4, we have to take VR2 as the V (source voltage) because R4 and R5 are in series but R2 is in parallel with R4 and R5. It is also proven by using KVL: VR2 = VR4 + VR5. VR5 is not equal to VR2 because there is a voltage drop across R4 or simply VR5 = VR2 – VR4.

 

Example 1

By referring to the circuit below, find VR8.

In order to find VR8, we need to know VR7. To know VR7, we need to calculate VR3 and to calculate VR3; we have to calculate VR1 but VR1 is equal to V because they are connected in parallel.

VR1 = V

 

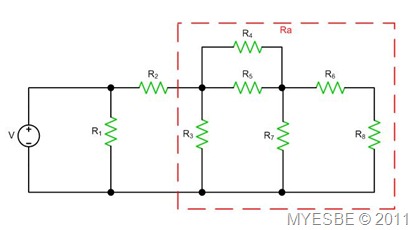
To get VRa;

VRa = [Ra/(R2+Ra)]*V

VR3 = VRa

 

 

VRc = [Rc/(Rb + Rc)]*VRa; VRc = VR7

VR8 = [R8/(R6 + R8)]*VRc;