Equivalent Resistances (Basic circuit: Series and parallel connections)

 

Equivalent resistance is basically the total resistance from two nodes (says node ‘a’ and ‘b’). In order to get the total resistance at a certain node, two basic connections need to be understood beforehand. The connections are series and parallel.

Figure 1: Series connection

 

Figure 2: Parallel connection

 

Let’s analyze both circuits. For series circuit, R₁ connected to R₂ without the existence of any junction in between them. For parallel circuit, both legs of R₁ and R₂ are connected together. Now, we have to know how to simplify the circuit from two resistor become only one resistor (total resistor).

Series circuit:

R_ab = R₁ + R₂

Parallel circuit:

R_ab = (R₁*R₂)/(R₁+R₂)

 

Example 1

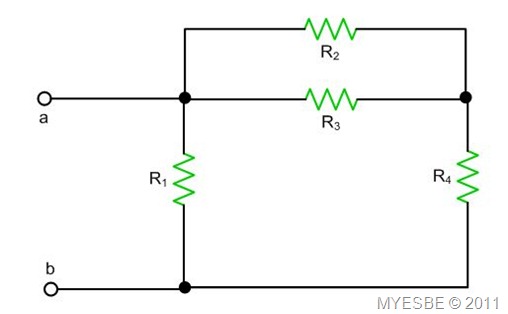
From the figure below, find the total resistance, R_ab.

 

Two common questions will normally be asked:

1) Where should we start?

2) Which formula to use?

To start simplifying the circuit, we need to find where the resistors that are connected in series and parallel are.

Look at R₁, is it connected parallel with R₄? No, it isn’t because there is R₃ that block R₄ to connect to R₁. Hence, only one of the R₄ leg is connected to R₁ and another leg is not directly connected to R₁. So, we cannot start simplifying our circuit from R₁.

Look at R₂, is it connected parallel with R₃? Yes, it is because both R₂ legs are connected to both R₃ legs. So, we can start simplifying our circuit from R₂ and R₃. Now, let’s ask the second question. Which formula to use? Of course we have to use parallel total resistance’s formula.

R_2&3 = (R₂*R₃)/(R₂+R₃)

 

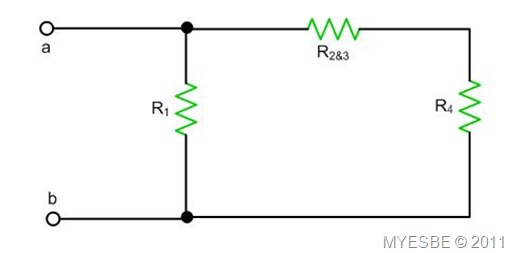
Again, to simplify the circuit, we need to find where the resistors that are connected in series or parallel are.

Look at R₁, is it connected parallel with R₄? No, it isn’t because there is R_2&3 that block R₄ to connect to R₁. Hence, only one of the R₄ leg is connected to R₁ and another leg is not directly connected to R₁. So, we cannot simplify our circuit from R₁.

Look at R_2&3, is it connected parallel with R₄? No, it isn’t but it is connected in series with R₄ because there is no branch in between them. So, we can simplify our circuit for R_2&3 and R₄. Now, let’s ask the second question. Which formula to use? Of course we have to use series total resistance’s formula.

R_2&3&4 = R_2&3 + R₄

 

 

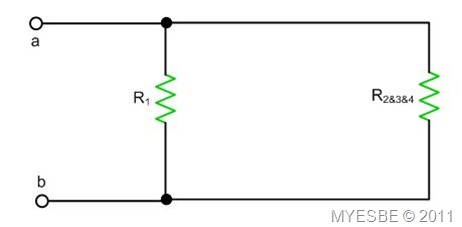
Now, obviously from the figure, both resistors are connected in parallel. Therefore,

R_ab = R_1&2&3&4 = (R₁*R_2&3&4)/(R₁+R_2&3&4)

 

 

Example 2

From the figure below, find the total resistance, R_ab.

 

 

 

 

 

R_ab = ([([(R₆ + R₇)//R₅] + R₄)//R₃] + R₂)//R₁

Where ‘+‘ = series resistor and ‘//’ = parallel resistor

 

Example 3

From the figure below, find the total resistance, R_ab.

 

 

 

 

 

 

Rab = ([([(R₆ + R₈)//R₇] + [R₄//R₅])//R₃] + R₂)//R₁